Econometria de séries temporais

Objetivo do curso

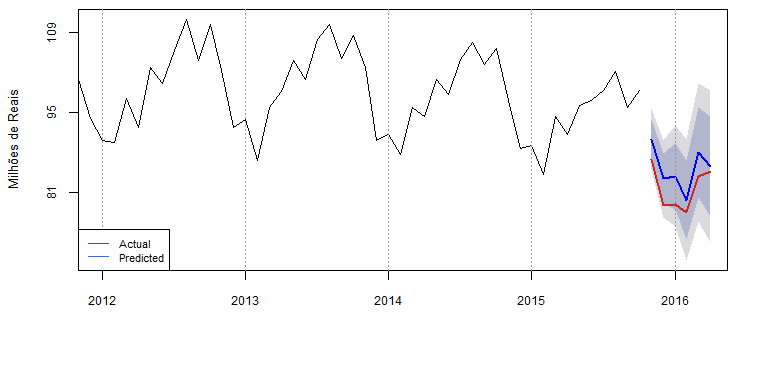
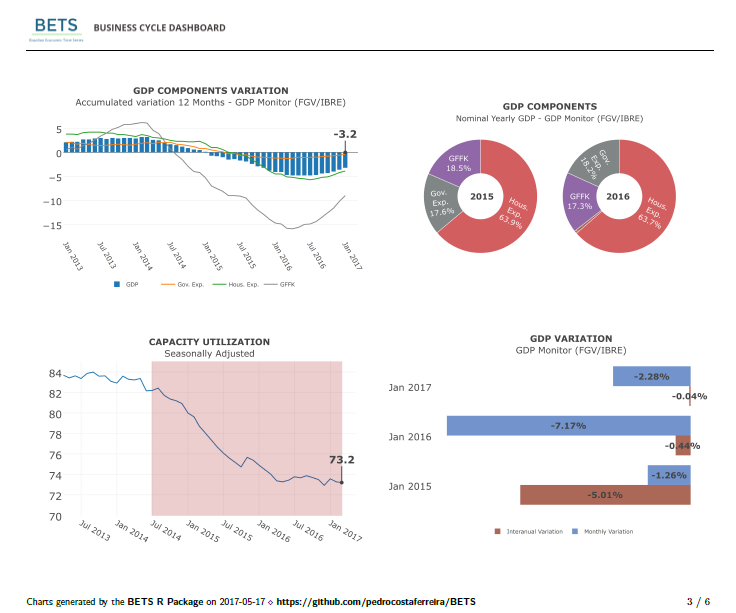
Estudar os principais modelos univariados de Séries Temporais(Modelos Box & Jenkins, modelos GARCH etc), modelos econométricos multivariados (Modelos VAR, VECM) e aplicar os conceitos desenvolvidos no software R. Almeja-se, assim, transmitir os conhecimentos de modelagem estatística, análise de sensibilidade e previsão de séries temporais como, por exemplo, séries de vendas, receitas, despesas, preços, demanda, entre outras.

Preliminares

  • a) Considerações Gerais;
  • b) Algumas Séries Temporais
  • c) Objetivos da Análise de Séries Temporais
  • d) Roteiro do curso
  • e) Processos Estoc´asticos
  • f) Estacionariedade
  • g) Autocovariância e Autocorrelação
  • h) Ergodicidade
  • i) Ruído Branco

2.

  • a) Processos Auto-Regressivos - AR(p)
  • b) Processos Médias Móveis MA(q)
  • c) Processos Auto-Regressivos de Médias Móveis ARMA(p,q)
  • d) Função de Autocorrelação - FAC
  • e) Funçãao de Autocorrelação Parcial FACP
  • f) Identificação
  • g) Estimação
  • h) Diagnóstico dos Resíduos
  • i) Previsão
Clique aqui para ver a ementa completa do curso em PDF.

Abaixo segue as três listas de exercícios disponíveis no meu repositório dedicado a ecometria de séries temporais. Você pode acessar todo o material aqui:

Estatística 1

Apresentar uma abordagem conceitual, prática e aplicada em Análise de Dados, Estatística Descritiva, Probabilidades, Distribuições de Probabilidade, Teoria da Amostragem e Inferência Estatística. Ainda, será apresentada a teoria de Números Índices, importante tópico estatístico relacionado a índices de preço.

Objetivo do curso

Ao final do curso espera-se que o aluno tenha um conhecimento básico das técnicas estatísticas apresentadas, estando apto a aplicar as diferentes técnicas e utilizá-las como ferramentas de análise e tomada de decisão.


  • 1) Análise, descrição e interpretação de dados: tabelas de distribuição de frequência e gráficos
  • 2) Medidas de posição ou tendência central para dados discretos e agrupados;
  • 3) Medidas de variação para variáveis discretas e contínuas;
  • 4) Medidas de assimetria e curtose
  • 5) Análise Bidimensional
  • 6) Probabilidade: variáveis aleatórias discretas e contínuas, propriedades
  • 7) Distribuições de probabilidade e aplicações para variáveis discretas: Uniforme, Bernoulli, Binomial, Poisson;
  • 8) Distribuições de probabilidade e aplicações para variáveis contínuas: Uniforme, Normal, Normal Padrão, Exponencial
  • 9) Teoria da Amostragem
  • 10) Números Índices


© 2017 - Pedro costa ferreira