

Vamos modelar a série de produção de bens intermediários (PBI) com o BETS usando a metodologia Box & Jenkins. No final, seremos capazes de usar o modelo para fazer previsões.
O método de Box & Jenkins permite que os valores futuros da série em estudo sejam previstos somente com base nos valores passados e presentes da mesma série, isto é, as previsões são feitas a partir de modelos univariados.
Estes modelos são chamados SARIMA, uma sigla para o termo em inglês Seasonal Auto-Regressive Integrated Moving Average, e têm a forma:
ΦP(B)ϕp(B)∇d∇DZt = ΘQ(B)θq(B)at
onde
Em sua concepção original, que será adotada aqui, a metodologia de Box & Jenkins se divide em três estágios iterativos:
Se o modelo não for aprovado na fase (iii), volta-se ao passo (i). Caso contrário, o modelo pode ser utilizado para fazer previsões. Na próxima seção, conforme o exemplo for evoluindo, cada um desses estágios será observado de perto e mais será dito sobre a metodologia.
O primeiro passo é encontrar a série PBI na base de dados do BETS. Isso
pode ser feito com a função BETS.search. O comando e sua saída são
mostrados abaixo.
> # Busca em português pela série de produção de bens intermediários
> results = BETS.search(description = "'bens intermediarios'", lang = "pt", view = F)
> results
## code
## 1 1334
## 2 11068
## 3 21864
## 4 25302
## 5 25328
## description
## 1 Indicadores da produção (1991=100) - Por categoria de uso - Bens intermediários
## 2 Indicadores da produção (2002=100) - Por categoria de uso - Bens intermediários
## 3 Indicadores da produção (2012=100) - Bens intermediários
## 4 Importações - Bens intermediários (CGCE)
## 5 Importações (kg) - Bens intermediários (CGCE)
## unit periodicity start source
## 1 Índice M 31/01/1975 IBGE
## 2 Índice M 31/01/1991 IBGE
## 3 Índice M 01/01/2002 IBGE
## 4 US$ M 01/01/1997 MDIC/Secex
## 5 kg M 01/01/1997 MDIC/Secex
Agora, carregamos a série através da função BETS.get e guardamos
alguns valores para, posteriormente, comparar com as previsões do modelo
que será estabelecido. Também criaremos um gráfico (figura ), pois ele
ajuda a formular hipóteses sobre o comportamento do processo estocástico
subjacente.
> # Obtenção da série de código 21864 (Produção de Bens Intermediários, IBGE)
> data <- BETS.get(21864)
>
> # Guardar últimos valores para comparar com as previsões
> data_test <- window(data, start = c(2015,11), end = c(2016,4), frequency = 12)
> data <- window(data, start = c(2002,1), end = c(2015,10), frequency = 12)
> # Gráfico da série
> plot(data, main = "", col = "royalblue", ylab = "PBI (Número Índice)")
> abline(v = seq(2002,2016,1), col = "gray60", lty = 3)
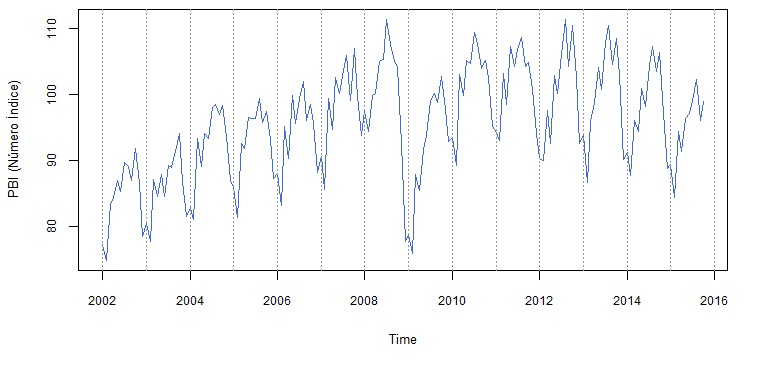
Gráfico da série de produção de bens intermediários no Brasil.
Quatro características ficam evidentes. Primeiramente, trata-se de uma série homocedástica e sazonal na frequência mensal. Este último fato é corroborado pelo gráfico mensal da série (figura ), que mostra o nível de produção por mês (a média é a linha tracejada).
> # Gráfico mensal da série
> monthplot(data, labels = month.abb, lty.base = 2, col = "red",
+ ylab = "PBI (Número Índice)", xlab = "Month")
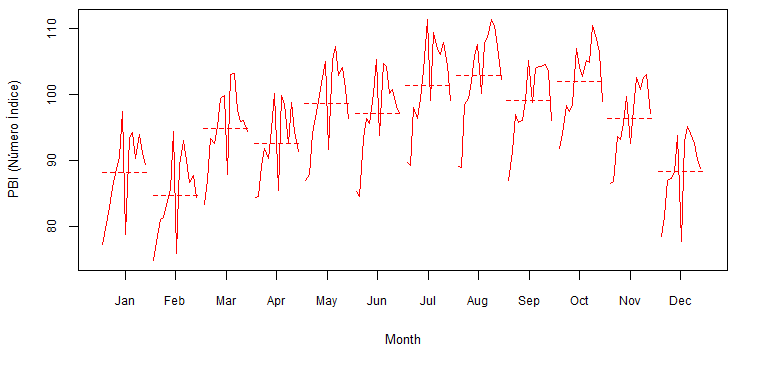
Gráfico mensal da série em estudo.
Um terceiro aspecto marcante da série é a quebra estrutural em novembro de 2008, quando ocorreu a crise financeira internacional e a confiança dos investidores despencou. A quebra impactou diretamente na quarta característica importante da série: a tendência. Incialmente, a tendência era claramente crescente, mas não explosiva. A partir de novembro de 2008, porém, parece que o nível da série se manteve constante ou até mesmo descresceu. Em um primeiro momento, a quebra estrutural será desconsiderada na estimação dos modelos, mas logo o benefício de levá-la em conta explicitamente ficará claro.
A seguir, criaremos um modelo para a série escolhida de acordo com os passos definidos anteriormente.
Esta subseção trata de um passo crucial na abordagem de Box & Jenkins: a determinação da existência e da quantidade total de raízes unitárias no polinômio autorregressivo não-sazonal e sazonal do modelo. De posse desses resultados, obtemos uma série estacionária através da diferenciação da série original. Assim, poderemos identificar a ordem dos parâmetros através da FAC e FACP, pois isso deve feito através de séries estacionárias de segunda ordem.
A função BETS.ur_test executa o teste Augmented Dickey Fuller (ADF).
Ela foi construída em cima da função ur.df do pacote urca, que é
instalado juntamente com o BETS. A vantagem da BETS.ur_test é a saída,
desenhada para que o usuário visualize rapidamente o resultado do teste
e tenha todas as informações de que realmente necessita. Trata-se de um
objeto com dois campos: uma tabela mostrando as estatísticas de teste,
os valores críticos e se a hipótese nula é rejeitada ou não, e um vetor
contendo os resíduos da equação do teste. Esta equação é mostrada
abaixo.
Δyt = ϕ + τ1t + τ2yt − 1 + δ1Δyt − 1 + ⋯ + δp − 1Δyt − p + 1 + εt
As estatísticas de teste da tabela do objeto de saída se referem aos
coeficientes ϕ (média ou drift), τ1 (tendência
determinística) e τ2 (raiz unitária). A inclusão da média e
da tendência determinística é opcional. Para controlar os parâmetros do
teste, a BETS.ur_test aceita os mesmos parâmetros da ur.df, além do
nível de significância desejado.
> df = BETS.ur_test(y = data, type = "drift", lags = 11,
+ selectlags = "BIC", level = "5pct")
>
> # Exibir resultado dos testes
> df$results
## statistic crit.val rej.H0
## tau2 -2.420907 -2.88 no
## phi1 3.531397 4.63 yes
Portanto, para a série em nível, observa-se que não se pode rejeitar a
hipotése nula de existência de uma raiz unitária ao nível de confiança
de 95%, pois a estatística de teste é maior do que o valor crítico.
Agora, iremos aplicar a função diff à série repetidas vezes e
verificar se a série diferenciada possui uma raiz unitária.
> ns_roots = 0
> d_ts = diff(data)
>
> # Loop de testes de Dickey-Fuller.
> # A execução é interrompida quando não for possível rejeitar a hipótese nula
> while(df$results[1,"statistic"]> df$results[1,"crit.val"]){
+ ns_roots = ns_roots + 1
+ d_ts = diff(d_ts)
+ df = BETS.ur_test(y = d_ts, type = "none", lags = 11,
+ selectlags = "BIC", level = "5pct")
+ }
>
> ns_roots
## [1] 1
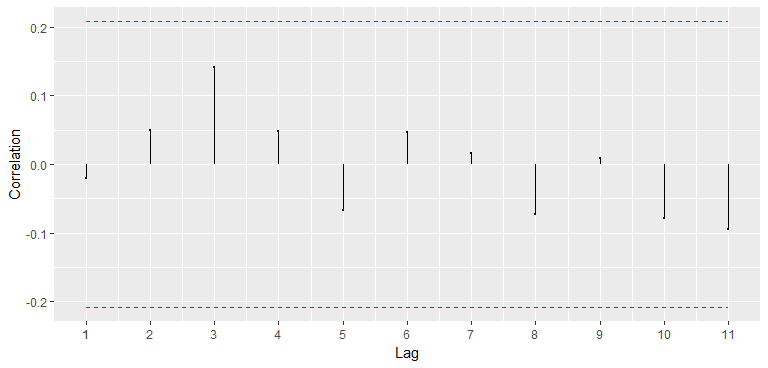
Logo, para a série em primeira diferença, rejeita-se a hipótese nula de que há raiz unitária a 5% de significância. A FAC dos resíduos da equação do teste evidencia que ele foi bem especificado, pois a autocorrelação não é significativa até a décima primeira defasagem.
> # Fazer FAC dos resíduos, com intervalo de confiança de 99%
> BETS.corrgram(df$residuals,ci=0.99,style="normal",lag.max = 11)
Um outro pacote bastante útil que é instalado com o BETS é o forecast.
Usaremos a função nsdiffs deste pacote para realizar o teste de
Osborn-Chui-Smith-Birchenhall e identificar raízes unitárias na
frequência sazonal (em nosso caso, mensal).
> library(forecast)
>
> # Testes OCSB para raízes unitárias na frequencia sazonal
> nsdiffs(data, test = "ocsb")
## [1] 1
Infelizmente, a nsdiffs não fornece nenhuma outra informação sobre o
resultado do teste além do número de diferenças sazonais que devem ser
tiradas para eliminar as raizes unitárias. Para o caso da série em
análise, o programa indica que não há raiz unitária mensal, não sendo
necessária, portanto, diferenças nesta frequência.
As conclusões anteriores são corroboradas pela função de autocorrelação da série em primeira diferença (figura ). Ela mostra que autocorrelações estatisticamente significativas, isto é, fora do intervalo de confiança, não são persistentes para defasagens múltiplas de 12 e no entorno destas, indicado a ausência da raiz unitária sazonal.
As funções do BETS que utilizamos para desenhar correlogramas é a
BETS.corrgram. Diferentemente de sua principal alternativa, a Acf do
pacote forecast, a BETS.corrgram retorna uma gráfico atraente e
oferece a opção de calcular os intervalos de confiança de acordo com a
fórmula proposta por Bartlett. Sua maior vantagem, contudo, não pôde ser
exibida aqui, pois depende de recursos em flash. Caso o parâmetro
style seja definido como 'plotly', o gráfico torna-se interativo e
mostra todos os valores de interesse (autocorrelações, defasagens e
intervalos de confiança) com a passagem do mouse, além de oferecer
opções de zoom, pan e para salvar o gráfico no formato png.
> # Correlograma de diff(data)
> BETS.corrgram(diff(data), lag.max = 48, mode = "bartlett", style="plotly", knit = T)
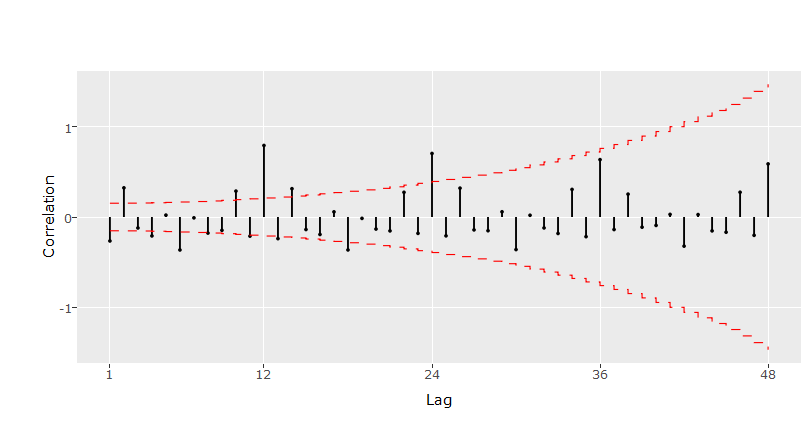
Função de Autocorrelação de *∇Z*t**
O correlograma acima ainda não é suficiente para determinamos um modelo
para a série. Faremos, então, o gráfico da função de autocorrelação
parcial (FACP) de ∇Z*t*. A BETS.corrgram também pode ser
utilizada para este fim.
> # Função de autocorrelação parcial de diff(data)
> BETS.corrgram(diff(data), lag.max = 36, type = "partial", style="plotly", knit = T)
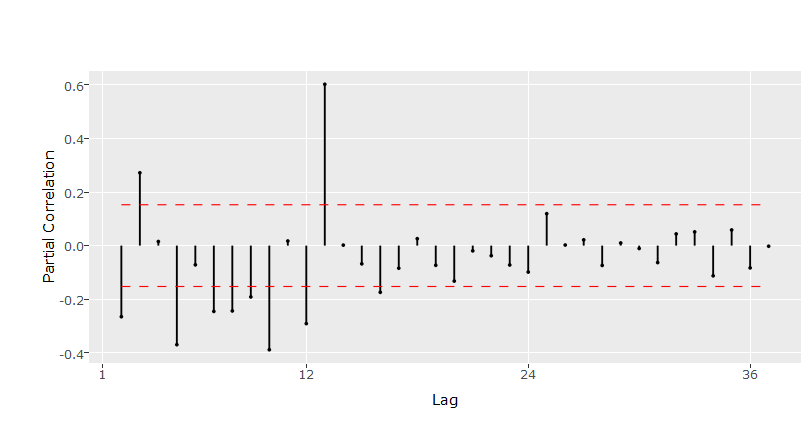
Função de Autocorrelação Parcial de *∇Z*t**
A FAC da figura e a FACP da figura podem ter sido geradas por um
processo SARIMA(0,0,1) (0,0,1). Esta conjectura se baseia na
observação de que as defasagens múltiplas de 12 parecem apresentar corte
brusco na FACP a partir da segunda (isto é, a de número 24) e decaimento
exponencial na FAC. Além disso, as duas primeiras defasagens da FAC
parecem significativas, enquanto as demais, não. Há, ainda, alguma
evidência de decaimento exponencial na FACP, exceto na frequência
sazonal. Os dois últimos fatos indicam que o polinômio de médias móveis
(não sazonal) pode ter ordem 2. Por estas razões, o primeiro modelo
proposto para Z*t* será um SARIMA(0,1,1)(0,1,1)[12].
Para estimar os coeficientes do modelo SARIMA(0,1,1)(0,1,1)[12], será
aplicada a função Arima do pacote forecast. Os testes t serão feitos
através da função BETS.t_test do BETS, que recebe um objeto do tipo
arima ou Arima, o número de variáveis exógenas do modelo e o nível
de significância desejado, devolvendo um data.frame contendo as
informações do teste e do modelo (coeficientes estimados, erros padrão,
estatísticas de teste, valores críticos e resultados dos testes).
> # Estimacao dos parâmetros do modelo
> model1 = Arima(data, order = c(0,1,1), seasonal = c(0,1,1))
>
> # Teste t com os coeficientes estimados
> # Nível de significância de 1%
> BETS.t_test(model1, alpha = 0.01)
## Coeffs Std.Errors t Crit.Values Rej.H0
## ma1 -0.2242623 0.07004662 3.201615 2.606518 TRUE
## sma1 -0.8603049 0.08797294 9.779199 2.606518 TRUE
Concluímos pela coluna Rej.H0 que os dois coeficientes do modelo,
quando estimados por máxima verossimilhança, são estatisticamente
significativos a 99% de confiança.
O objetivo dos testes de diagnóstico é verificar se o modelo escolhido é adequado. Neste trabalho, duas conhecidas ferramentas serão empregadas: a análise dos resídos padronizados e o teste de Llung-Box.
O gráfico dos resíduos padronizados (figura ) será feito com o auxílio
da função BETS.std_resid, que foi implementada especificamente para
isso.
> # Gráfico dos resíduos padronizados
> resids = BETS.std_resid(model1, alpha = 0.01)
>
> # Evidenciar outlier
> points(2008 + 11/12, resids[84], col = "red")
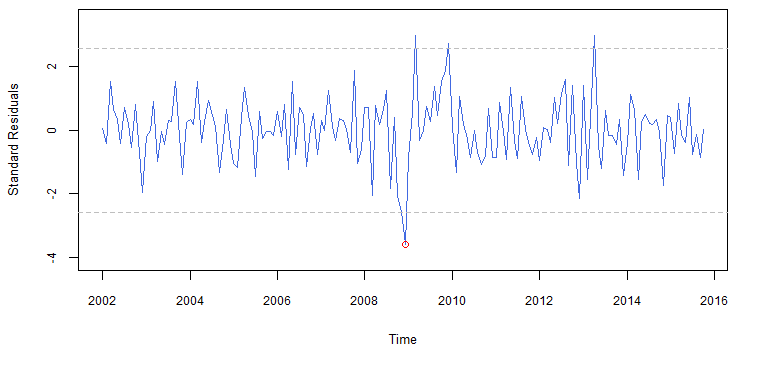
Resíduos padronizados do primeiro modelo proposto
Observamos que há um outlier proeminente e estatisticamente significativo em novembro de 2008. Este ponto corresponde à data da quebra estrutural que identificamos na figura . Portanto, foi proposto um segundo modelo, que inclui uma dummy definida como se segue:
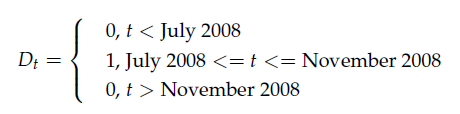
Esta dummy pode ser criada com a função BETS.dummy, como mostramos
abaixo. Os parâmetros start e end indicam o início e o fim do
período coberto pela dummy, que nada mais é que uma série temporal
cujos valores podem ser apenas 0 ou 1. Os campos from e to indicam o
intervalo em que a dummy deve assumir valor 1.
> dummy = BETS.dummy(start = c(2002,1), end = c(2015,10), from = c(2008,9), to = c(2008,11))
> dummy
## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 2002 0 0 0 0 0 0 0 0 0 0 0 0
## 2003 0 0 0 0 0 0 0 0 0 0 0 0
## 2004 0 0 0 0 0 0 0 0 0 0 0 0
## 2005 0 0 0 0 0 0 0 0 0 0 0 0
## 2006 0 0 0 0 0 0 0 0 0 0 0 0
## 2007 0 0 0 0 0 0 0 0 0 0 0 0
## 2008 0 0 0 0 0 0 0 0 1 1 1 0
## 2009 0 0 0 0 0 0 0 0 0 0 0 0
## 2010 0 0 0 0 0 0 0 0 0 0 0 0
## 2011 0 0 0 0 0 0 0 0 0 0 0 0
## 2012 0 0 0 0 0 0 0 0 0 0 0 0
## 2013 0 0 0 0 0 0 0 0 0 0 0 0
## 2014 0 0 0 0 0 0 0 0 0 0 0 0
## 2015 0 0 0 0 0 0 0 0 0 0
Como podemos ver nos resultados da execução do trecho de código a seguir, a estimação deste modelo através de máxima verossimilhança resultou em coeficientes estatisticamente diferentes de 0 ao nível de significância de 5%, inclusive para a dummy. O gráfico dos resíduos padronizados dos valores ajustados pelo novo modelo (figura ) também mostra que a inclusão de Dt foi adequada, uma vez que não há mais evidência de quebra estrutural.
> # Estimacao dos parâmetros do modelo com a dummy
> model2 = Arima(data, order = c(0,1,1), seasonal = c(0,1,1), xreg = dummy)
>
> # Teste t com os coeficientes estimados
> # Nível de significância de 1%
> BETS.t_test(model2, alpha = 0.01)
## Coeffs Std.Errors t Crit.Values Rej.H0
## ma1 -0.2142085 0.06950419 3.081951 2.606518 TRUE
## sma1 -0.8374282 0.08608494 9.727929 2.606518 TRUE
## dummy 4.0920955 1.56375356 2.616842 2.606518 TRUE
> resids = BETS.std_resid(model2, alpha = 0.01)
>
> # Evidenciar novembro de 2008
> points(2008 + 11/12, resids[84], col = "red")
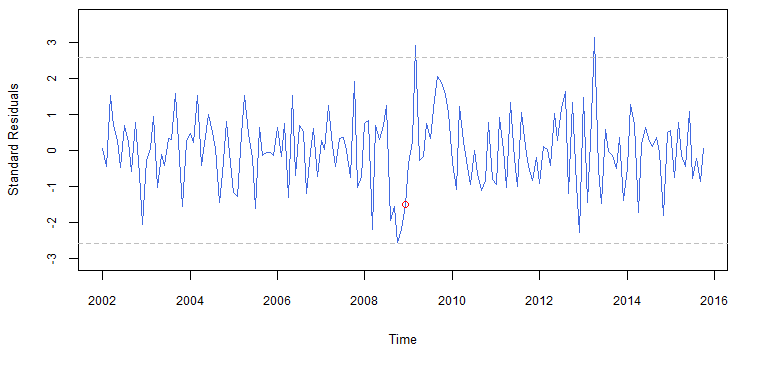
Resíduos padronizados do modelo proposto após a detecção de quebra estrutural
> # Mostrar BIC dos dois modelos estimados
> model1$bic
## [1] 726.7885
> model2$bic
## [1] 725.1295
Notamos, ainda, que o Bayesian Information Criteria (BIC) do modelo com a dummy é menor. Logo, também por este critério, o modelo com a dummy deve ser preferido ao anterior.
O teste de Ljung-Box para o modelo escolhido pode ser executado através
da função Box.test do pacote stats. Para confirmar o resultado dos
testes, fazemos os correlogramas dos resíduos e vemos se há algum padrão
de autocorrelação.
> # Teste de Ljung-Box nos resíduos do modelo com a dummy
> boxt = Box.test(resid(model2), type = "Ljung-Box",lag = 2)
> boxt
##
## Box-Ljung test
##
## data: resid(model2)
## X-squared = 1.1446, df = 2, p-value = 0.5642
> # Correlograma dos resíduos do modelo com a dummy
> BETS.corrgram(resid(model2), lag.max = 20, mode = "bartlett", style = "normal")
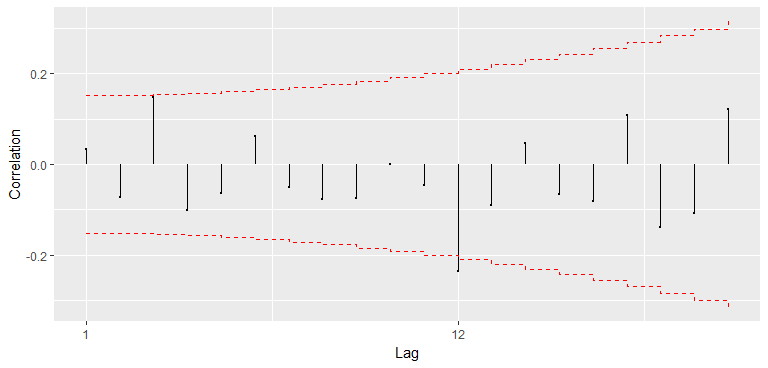
Função de autocorrelação dos resíduos do modelo com a {}.
O p-valor de 0.4529 indica que há grande probabilidade de a hipótese nula de que não há autocorrelação nos resíduos não seja rejeitada. Parece ser o caso, como mostra a figura . Concluímos, então, que o modelo foi bem especificado.
O BETS fornece uma maneira conveniente para fazer previsões de modelos
SARIMA. A função BETS.predict recebe os parâmetros da função
forecast do pacote homônimo ou da BETS.grnn.test (a ser tratada
adiante, no segundo estudo de caso) e devolve não apenas os objetos
contendo as informações da previsão, mas também um gráfico da série com
os valores preditos. Essa visualização é importante para que se tenha
uma ideia mais completa da adequação do modelo. Opcionalmente, podem
também ser mostrados os valores efetivos do período de previsão.
Chamaremos a BETS.predict para gerar as previsões do modelo proposto.
Os parâmetros object (objeto do tipo arima ou Arima), h
(horizonte de previsão) e xreg (a dummy para o período de previsão)
são herdados da função forecast. Os demais são da própia
BETS.predict, sendo todos parâmetros do gráfico, com exceção de
actual, os valores efetivos da série no período de previsão.
> new_dummy = BETS.dummy(start = start(data_test), end = end(data_test))
>
> preds = BETS.predict(object = model2, xreg = new_dummy,
+ actual = data_test, xlim = c(2012, 2016.2), ylab = "Milhões de Reais",
+ style = "normal", legend.pos = "bottomleft")
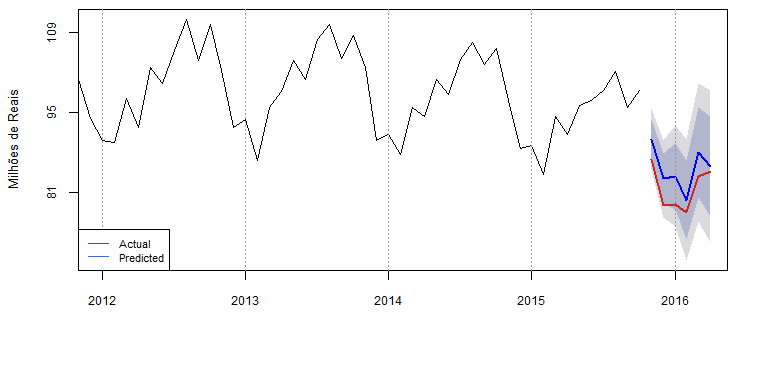
Gráfico das previsões do modelo SARIMA proposto.
As áreas em azul em torno da previsão são os intervalos de confiança de
85% (azul escuro) e 95% (azul claro). Parece que a aderência das
previsões foi satisfatória. Para dar mais significado a esta afirmação,
podemos verificar várias medidas de ajuste acessando o campo
'accuracy' do objeto retornado.
> preds[['accuracy']]
## ME RMSE MAE MPE MAPE ACF1
## Test set -5.383763 5.518828 5.383763 -6.579101 6.579101 -0.7219499
## Theil's U
## Test set 1.201717
o outro campo deste objeto, 'predictions', contém o objeto retornado
pela forecast (ou pela BETS.grnn.test, se for o caso). Na realidade,
este campo ainda conta com um dado adicional: os erros de previsão, caso
sejam fornecidos os valores efetivos da série no período de previsão.
A função BETS.report executa toda a modelagem Box & Jenkins para
qualquer conjunto de séries à escolha e gera relatórios com os
resultados, como foi dito no início desta seção. Ela permite que as
previsões feitas através do modelo sejam salvas em um arquivo de dados
> parameters = list(
+ lag.max = 48,
+ n.ahead = 12 )
>
> BETS.report(ts = 21864, parameters = parameters)
O resultado abre automaticamente, na forma de um arquivo html.
© 2016 - Pedro costa ferreira